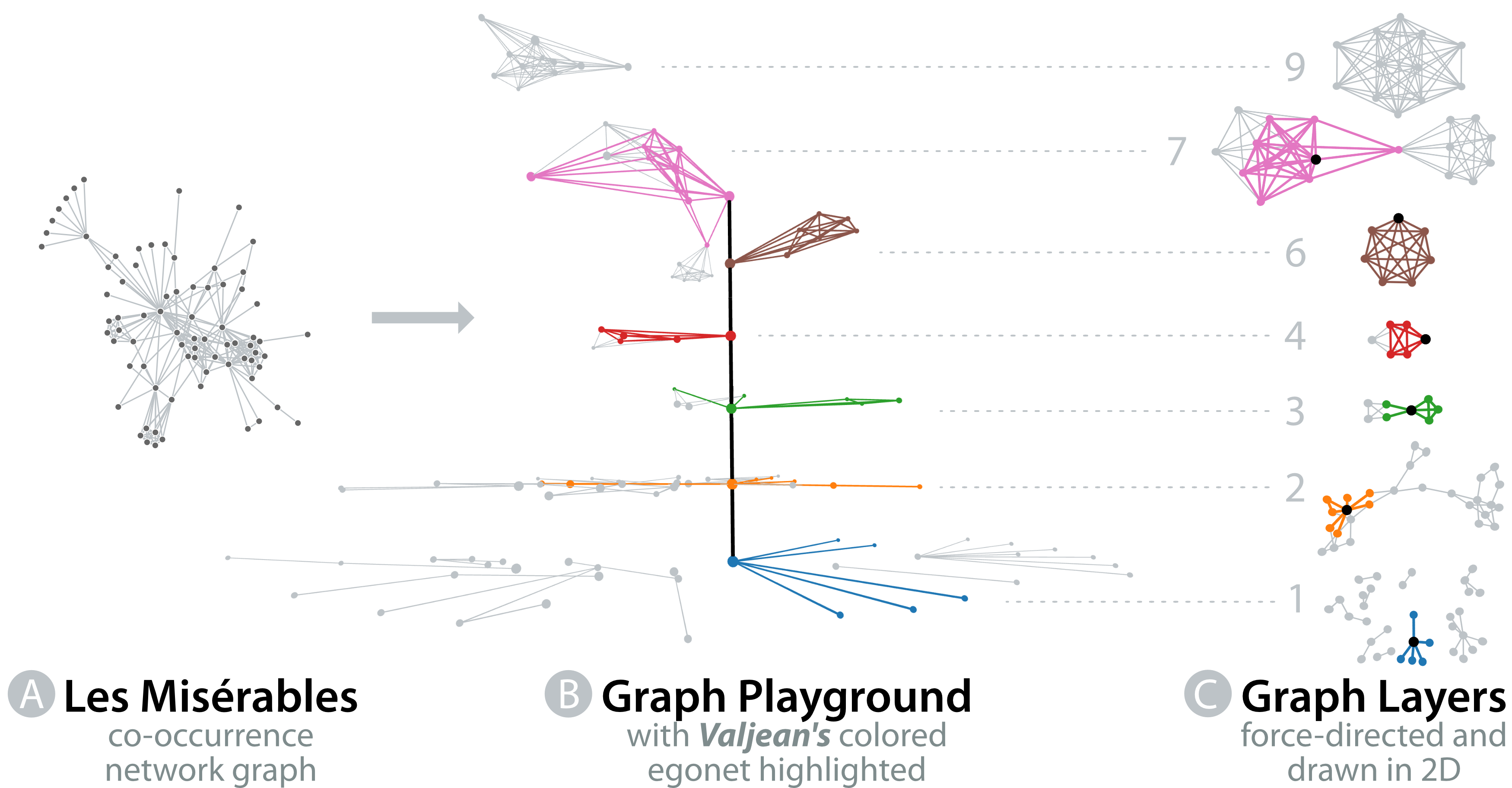
We use an iterative edge decomposition approach, derived from the popular iterative vertex peeling strategy, to globally split each vertex egonet (subgraph induced by a vertex and its neighbors) into a collection of edge-disjoint layers. Each layer is an edge maximal induced subgraph of minimum degree k that determines the layer density. This edge decomposition is derived completely from the overall network topology, and since each vertex can appear in multiple layers, we can associate to each vertex a vector profile that can be used to identify its different “roles” across the network. This allows us to explore a network’s topology at different levels of granularity, e.g., per layer and across layers. This is only feasible by mapping simultaneously a vertex to a set of 3D coordinates (x, y, and z) where the third coordinate encodes the different layers a vertex belongs to. This is one of the few instances where 3D visualization enhances graph exploration and navigation in an arguably “natural” way: a graph now becomes a 3D graph playground where a vertex plays a certain “role” per layer that is determined by the overall network topology. Our approach helps disentangle “hairball” looking embeddings produced by conventional 2D graph drawings.